Full 3-D Finite Element Analysis of a barrel's first few vibration mode shapes and frequencies calculated with the LS-DYNA code.

This is Mode #1 at 82.0 Hz
Note: Since most have broad band now, I have included the movie files on this
page.
![]() POSSIBLY MODE
SHAPES ARE NOT SO IMPORTANT.... I ran some FEA calculations of how a barrel
reacted to the high gas pressure and recoil. The forced deformations from the
high pressure gas and recoil cause the muzzle to change where it is pointing at
the target when the bullet exits the muzzle. Click on the graphic to read the
info on Esten's rifle. Esten did extensive testing so that the FEA model could
be normalized to his test data.
POSSIBLY MODE
SHAPES ARE NOT SO IMPORTANT.... I ran some FEA calculations of how a barrel
reacted to the high gas pressure and recoil. The forced deformations from the
high pressure gas and recoil cause the muzzle to change where it is pointing at
the target when the bullet exits the muzzle. Click on the graphic to read the
info on Esten's rifle. Esten did extensive testing so that the FEA model could
be normalized to his test data.

Click here or on the graphic to view the calculation
results.
| CONCLUSION.... Maybe the "consensus" was that a rifle barrel vibrated in one or more of the mode shapes when fired. That was because the mode shapes and frequencies were easy to calculate and they did seem to answer some of the questions. From these FEA dynamic pressure calculations, it appears that the recoil and forced deformations are much more important than the natural vibration modes in determining where a barrel is pointing when the bullet exits the muzzle. Then after the bullet exits the muzzle, the rifle barrel vibrates in its various natural frequencies and mode shapes. Put another way, consider a guitar string being plucked. One pulls the string into a position (forced position) then releases it and the string vibrates at is natural frequency. The recoil and bullet motions "pulls" the rifle barrel to a new shape and once the bullet leaves the barrel, then the barrel vibrates. However, the addition of the scope to the model has shown some small high frequency vibrations superimposed on the forced deformations, both of which, slightly alter where the muzzle points before the bullet exits. For lowering the amplitude of the high frequency vibrations, it appears that even an "out of tune" tuner is better than no tuner at all. |
This is a .308 caliber 1.25" to 0.9" diameter straight taper stainless steel barrel 22" long with the action end fixed. You are looking at the muzzle end and it is tilted down slightly for better viewing. These are the first 8 mode shapes and frequencies. Each bending mode (like Mode #1) is on one plane, but there was another identical mode in another plane at the same frequency that was not shown to save space. The torsional modes #4 and #8 are at a high frequency. I should have printed the mesh lines on the torsion modes so one could see the rotation. Note, modes 1, 2, 3, 6, and 7 are shown in a single plane, but can exist in other planes. Modes below a frequency of about 500 Hz will not be able to complete one full cycle before the bullet exits the barrel.
Barrel Harmonics Mode Shape Movies
| Mode Movie | Frequency (Hz) |
Mode Description |
| Mode #1 | 82.0 | Cantilever Bending |
| Mode #2 | 406 | 1 Node Bending |
| Mode #3 | 1050 | 2 Node Bending |
| Mode #4 | 1756 | Torsion |
| Mode #5 | 1984 | Axial Extension |
| Mode #6 | 2485 | 3 Node Bending |
| Mode #7 | 3180 | 4 Node Bending |
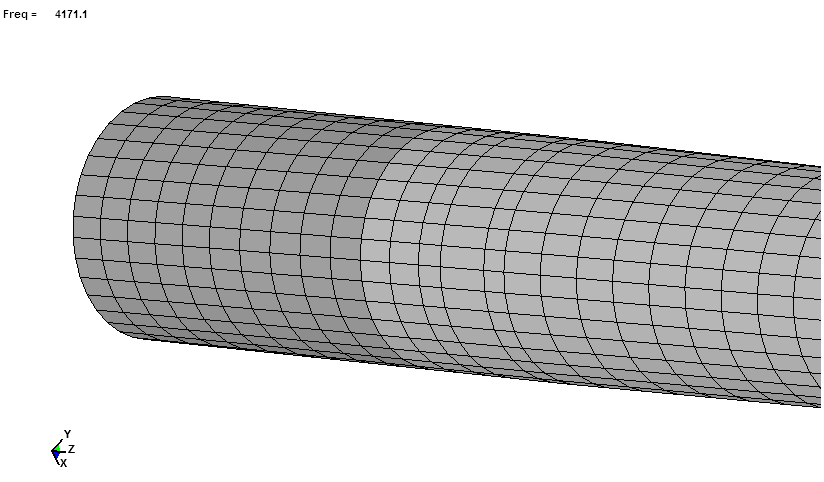
| Mode #8 | 4171 | 1 Node Torsion |
The amplitude of each mode shape's deflection is arbitrarily large to more clearly show the deformations.
| Mode 1 82.0 Hz |
 |
| Mode 2 406 Hz |
 |
| Mode 3 1050 Hz |
 |
| Mode 4 1756 Hz |
 |
| Mode 5 1984 Hz |
 |
| Mode 6 2485 Hz |
 |
| Mode 7 3180 Hz |
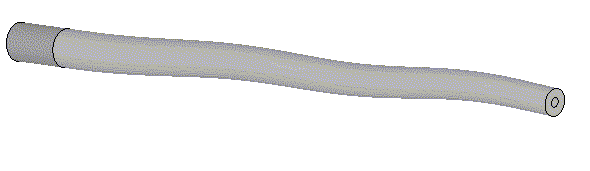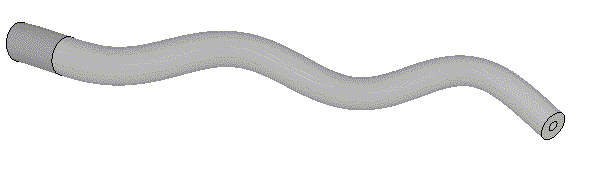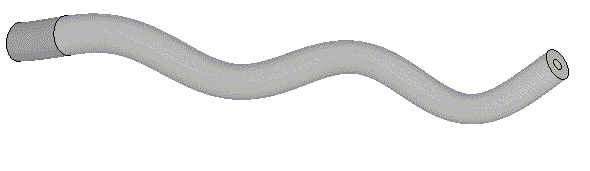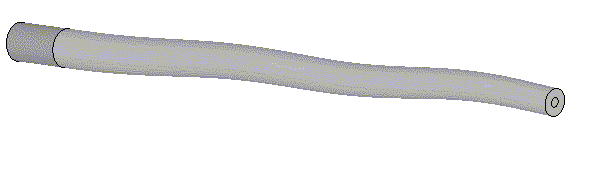 |
| Mode 8 4171 Hz |
 |
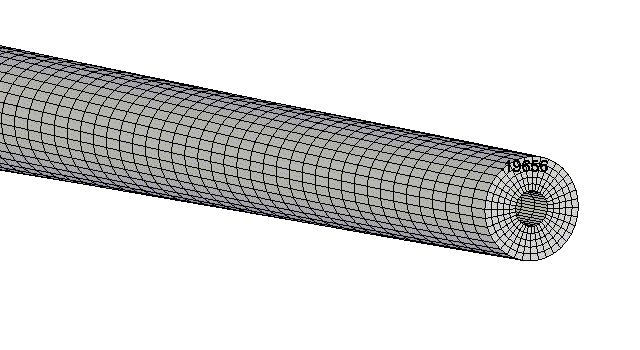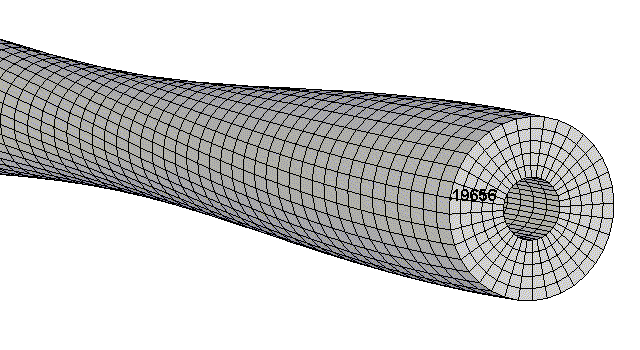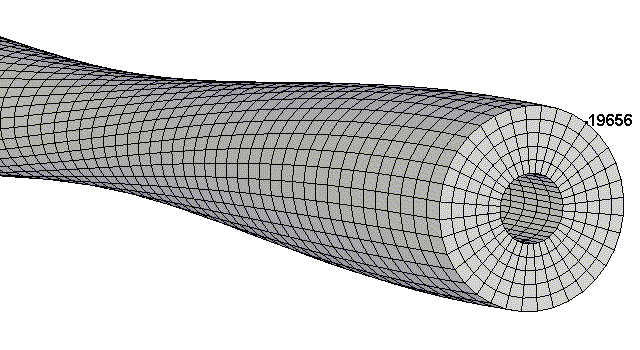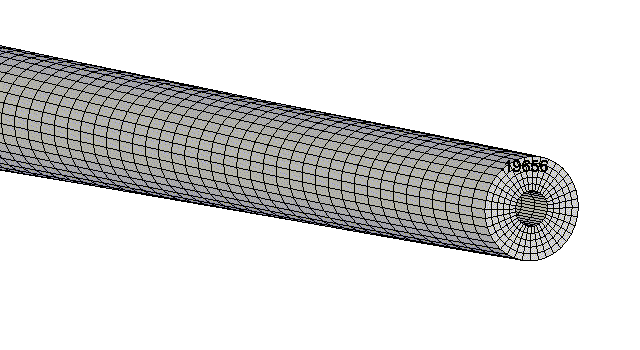
Here is Mode 8 with the mesh lines included. I also picked out a node on the
muzzle so one could see the rotation. Mode 4 also rotates.
What is hard to visualize here, is that all of these modes are excited and start from the step function load of firing a round. The higher frequency modes have extremely small amplitudes, but trying to visualize all of these modes at the same time with their different frequencies is mind boggling.
This is the outside of the section of the action and the barrel. The left edge
of the action was fixed to a rigid surface.
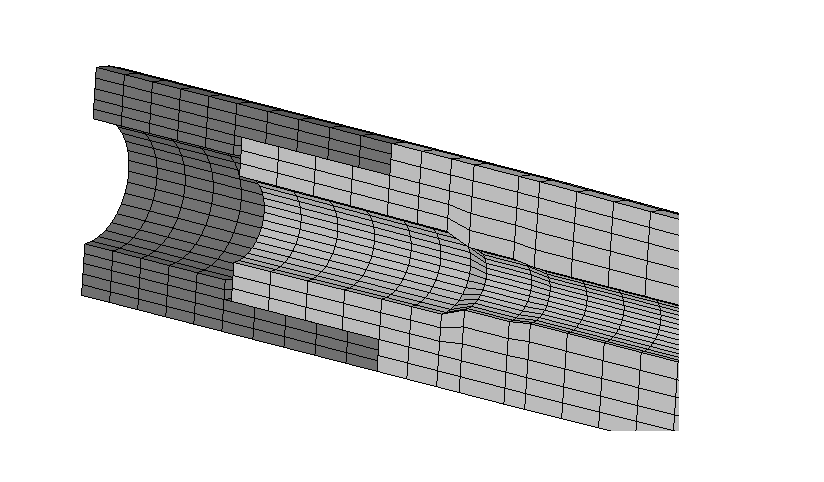
This shows the mesh detail of the action and the barrel. The chamber has the
dimensions of a 308 Win caliber. The threads were not used but the barrel tenon
was bonded to the action to simulate a threaded joint.
HOW ACCURATE?.... How well do the FEA codes calculate the mode vibration frequencies? Below is a table comparing the modal frequency calculations for the first 5 mode shapes of a steel cantilever beam with a 0.5" square cross section and a length of 20". The equation in Chapter One, from the Shock and Vibration Handbook (Third Edition) should be quite accurate since it uses a "fudge factor" for each mode to normalize the results to test data.
Modal Analysis Accuracy Comparison
Mode Frequencies in Hz
Steel Cantilever Beam 0.5" x 0.5" x 20" long
| Mode Number |
Shock Handbook Equation | NIKE2D Plane Stress 1280 Elements |
LS-DYNA 3-D 5000 Elements |
| 1 | 40.2 | 40.67 | 40.19 |
| 2 | 251 | 254.1 | 251.2 |
| 3 | 705 | 708.3 | 700.1 |
| 4 | 1380 | 1379 | 1363 |
| 5 | 2280 | 2260 | 2334 |
More info on a barrel's forced deformation here: Esten's Rifle Page.
End of Page![]()